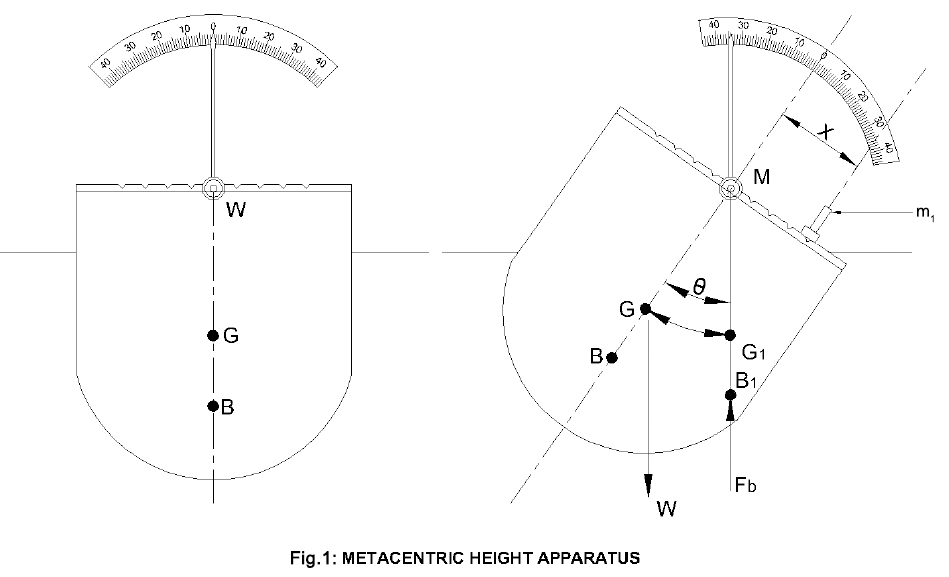
G = Centre of gravity of body
B = Centre of buoyancy of the body
M = Meta-centre of the body
\(m_1\) = Weight of hanger
x = Distance moved by weight \(m_1\)
θ = Angle of tilt
If a body is rotated by a slight angle, it begins to oscillate at the point around which it is inclined and that point is known as meta-centre. It is also defined as the intersection point of line of action of the buoyancy force (which is in the vertical direction) with the regular axis of the body when it is tilted through a small angular displacement. The distance between the meta-centre (denoted by ‘M’) and the centre of gravity (denoted by ‘G’) of the floating body is called the meta-centric height.
For a floating body to be in equilibrium on the liquid surface, it is important that not only the buoyant force (𝐹𝐵) and gravity force (𝑊) should be equal but also, the line of action of both forces must coincide, i.e., they should lie in the same vertical line. If the point M is above G, the floating body will be in stable equilibrium. When the floating body is given a slight angular displacement (say in clockwise direction), the position of the centre of buoyancy changes from B to B1 such that the line of action of the buoyant force passing through B1 cuts the axis at the point M, which is known as the meta-centre and the distance GM is known as the meta-centric height. The buoyant force 𝐹𝐵 acting through B1 and the weight force (W) of the body acting through G forms a couple acting in the counter-clockwise direction. This couple helps to restore the floating body back to its original position. To determine the meta-centric height of a floating body, we know the center of gravity of floating body. Place the hanger (m₁) over the center of the body. The hanger is moved across the vessel towards right through a distance x. The body will be tilted. The angle of tilt(θ) is measured using trigonometry. The new center of gravity of the body will shift to G₁ as the hanger has been moved towards the right and the center of buoyancy will change to B₁ as the body has tilted. Under equilibrium, the moment caused by the movement of the hanger through a distance x must be equal to the moment caused by the shift of the center of gravity from G to G₁.